Depth Constraint
Focal depth is a notoriously difficult parameter to resolve in any location algorithm because of the strong trade-off in most cases between focal depth and origin time. mloc has a number of tools with which to extract information on focal depth, subject to whatever limits the dataset imposes. There are three general cases:
- Focal depth can be resolved as a free parameter.
- Focal depth must be fixed, but a useful estimate can be made.
- No information on focal depth is available.
The most relevant commands in mloc are those used to specify which hypocentral parameters will be free in the inversion (freh and frec) and those that establish the starting depth for relocation (the dep_ family).
Free Depth
Focal depth can be included as a free parameter in the relocation of an earthquake when there is arrival time data at a range comparable to several times the focal depth or less. Schematically, what is required is at least one up-going raypath, which will have a partial derivative opposite in sign from that of the down-going raypaths that typically dominate arrival time datasets.
In order to set focal depth as a free parameter for a cluster, every event in the cluster should have suitable data to constrain its depth; otherwise the inversion is unlikely to converge. It is possible, using the frec command, to set depth free for some events and keep it fixed for others, but this has not been carefully tested and it may violate some assumptions of the code. A better strategy is to evaluate the subset of events that have depth control separately in a free depth relocation and then set the depths of those events accordingly (depm command) in a fixed-depth relocation of the entire cluster.
The Wells, Nevada cluster included in the mloc distribution is an example of a free-depth relocation
Fixed Depth, with Constraint
This is the most common scenario in practice. In the command file for a run each event definition section will include a member of the dep_ family that specifies the depth, its uncertainty and the source of the constraint. The different approaches to determining the depth at which an event should be constrained are discussed below. It is not unusual to have a few events in a cluster that must be set to the cluster default value (depc command), which is best determined by reference to those events in the cluster that do have good depth control.
The Mangyshlak PNE cluster included in the mloc distribution is an example of a relocation done this way. Constraints on the depths of the PNEs are available from Russian sources and the range of uncertainty in those values is small compared to the usual uncertainty in earthquake focal depths.
Most calibrated clusters in the GCCEL database have been relocated with fixed depth, but with most events having depth constraint of one sort or another.
No Constraint
Some clusters contain no events with depth control. These are typically clusters composed of relatively small events in remote areas with no local network data. It is often possible, however, to place some broad constraint on the likely range of depths based on seismotectonic considerations, and this in turn can be incorporated in mloc using a cluster default depth with the depc command.
The Jordan & Sverdrup Region A cluster included in the mloc distribution is an example of a relocation done this way. Earthquakes in oceanic intraplate settings have been observed as deep as 30 km or so, but in their original application of the Hypocentroidal Decomposition method to clusters in the south-central Pacific, Jordan and Sverdrup fixed all events at 10 km, influenced by the notion that the events were likely related to volcanism. For the purpose of comparison the same procedure is followed in our example cluster. In any case, the effect of moderate errors in depth for events located with teleseismic data is minor; depth mostly trades off with origin time. Since the water depth in the source region is about 5 km, the focal depths are about 5 km below the seafloor, in the oceanic crust.
In most cases, a cluster in which no event has depth control will also be one that cannot be calibrated.
Depth Reference Surface
In the global average travel-time model ak135 the zero level for depth is the reference ellipsoid WGS84. In other words, the zero depth reference surface is some distance below the land surface in most continental regions. Like all global location codes mloc normally makes a correction for station elevation (command corr), so the situation is straight-forward for a typical location analysis that uses regional or teleseismic data to estimate the hypocentroid of an event that is deep enough to be below the reference ellipsoid.
The situation gets more complicated if a direct calibration relocation is being done with events that are shallow enough that they may lie above the reference ellipsoid (for a cluster in the Tibet Plateau, for example, the events wouldn’t need to be all that shallow). In this case the corr command can be used to turn off station elevation corrections, which makes the reference surface for depth, roughly, the average elevation of the source region.
mloc is not suited to situations, such as volcano monitoring, where an event may be at a higher elevation than the stations being used to locate it.
Starting Depth
The value of starting depth for a relocation in mloc can be taken from several sources. The order of precedence (from most to least preferred) is:
- A dep_ command in the command file.
- Depth read from a .hdf file from a previous run.
- The depth from the input data file (if it carries a flag as being constrained).
- The value given with the depc command, if it has been given.
- The depth from the input data file (if a depth has been provided).
Methods of Constraining Focal Depth
If the available arrival time data are inadequate to resolve focal depth as a free parameter for all events in a cluster the relocation will probably need to be done with depths fixed, but it is still possible to determine focal depths for many events with a considerable degree of confidence outside the mloc relocation. There are four methods used in mloc that are based on the available arrival time data:
- Free-depth relocation of a subset of events
- Near-source readings
- Local distance readings
- Teleseismic depth phases (separate section)
There are also “external” sources of information on depth that can be used for constraint and mloc includes depth codes for most of the possibilities.
Free-Depth Relocation of a Subset of Events
If some events in a cluster are notable in having readings (say, from temporary stations) at very close range (within several focal depths) it is very worthwhile to form a subcluster for relocation in which depth can be left as a free parameter. In addition to providing very useful information on the likely depth range of the remainder of the cluster, the subcluster can be used to refine a local crustal model which can then be used in the “local-distance” method of depth constraint. The thickness of the crust of the crustal model cannot be reliably constrained unless at least some events have reasonable depth constraint. The depths from the free-depth relocation can be inserted into a subsequent command file as depm constraints in a fixed depth relocation of the larger cluster. mloc includes a command subc that helps in extracting the events that are most likely to behave well in such a subcluster.
Near-Source Readings
After a free-depth relocation the most powerful method of constraining focal depth utilizes readings at epicentral distances that are not much greater than the focal depth. Distances of 2 to 3 times the focal depth are still usable. There must be data (at greater distances, but only crustal arrivals) that constrains the epicenter closely for this to work; the near-source stations will not in themselves be sufficient. The relocation is done with depths fixed to match the near-source readings. Adjustment of focal depth and the crustal model proceed simultaneously. Arrivals at very close range are sensitive to depth more than velocity but the slope of arrival times of more distant crustal arrivals will be sensitive to average crustal velocity. When crustal arrivals (out to the Pg/Pn crossover, say, 100-150 km) are well-matched, the thickness of the crust is then adjusted to correctly predict the arrival times of Pn and Sn.
In many cases, manual adjustment of the focal depth in this manner is a more accurate method of constraining focal depth than a free-depth relocation, because it emphasizes the fit to the closest stations that are the most sensitive indicator of depth. In a free-depth location all the data used contributes to the estimation of depth, but residuals at greater distances are more likely to be distorted by lateral heterogeneity (or simply a less-accurate assumed crustal velocity model) which can be mapped into a biased estimate of depth. This is evident when a free-depth location leaves the closest stations with significant residuals.
Local Distance Readings
This method of constraining focal depths, unlike free-depth locations or fixing depth on the basis of a few near-source arrivals, will challenge the intuition of most seismologists, but it has been in regular use in mloc for over 5 years and has been applied to nearly every cluster in GCCEL (219 clusters and ~14,500 events at this writing). The local distance method has proven to be reliable and it greatly expands the number of events in calibrated clusters for which focal depth can be constrained at a useful level.
The key to understanding the method is to appreciate that it is not driven, as most “depth phases” are, by the depth derivative ∂t/∂h, but rather by the derivative of travel-time w.r.t. origin time. A set of circumstances are required that sound rather limiting but which are actually encountered quite commonly in practice. It is assumed that there are no near-source readings, say, within one or two (likely) focal depths, for the event in question or we would be setting depth by the method of fitting the near-source readings in a fixed-depth relocation, if not performing a free-depth inversion. On the other hand we do assume that there is at least one event in the cluster that does have good depth constraint, most commonly from near-source readings or a free-depth relocation of a subset of events that have the necessary data. This event (or preferably a good number of them) is termed a control event.
- For the event in question there must be at least one arrival of a direct crustal phase (Pg or Sg) at a distance less than the cross-over distance with Pn/Sn, i.e., the phase identification must be unambiguous.
- The average crustal velocity must have been adjusted to fit the observed slope of direct crustal arrivals as a function of distance, using control events. This is most easily checked with the near-source summary travel-time plot.
- The crustal thickness (Moho depth) must be constrained by considering the Pn arrivals from control events.
- A healthy population of Pn arrivals is needed for the event in question. Sn also contributes but with far less influence in most datasets.
Treated as a separate cluster in mloc, the control events can be accurately located using all readings for the cluster vectors and only direct crustal arrivals for the hypocentroid, i.e., a direct calibration. With Pg and Sg at short distances (within a couple focal depths) as well as greater distances, there is good constraint on depth in the normal manner. With depths set accurately, the direct crustal arrivals from the control events can be used to refine the crustal velocity model.
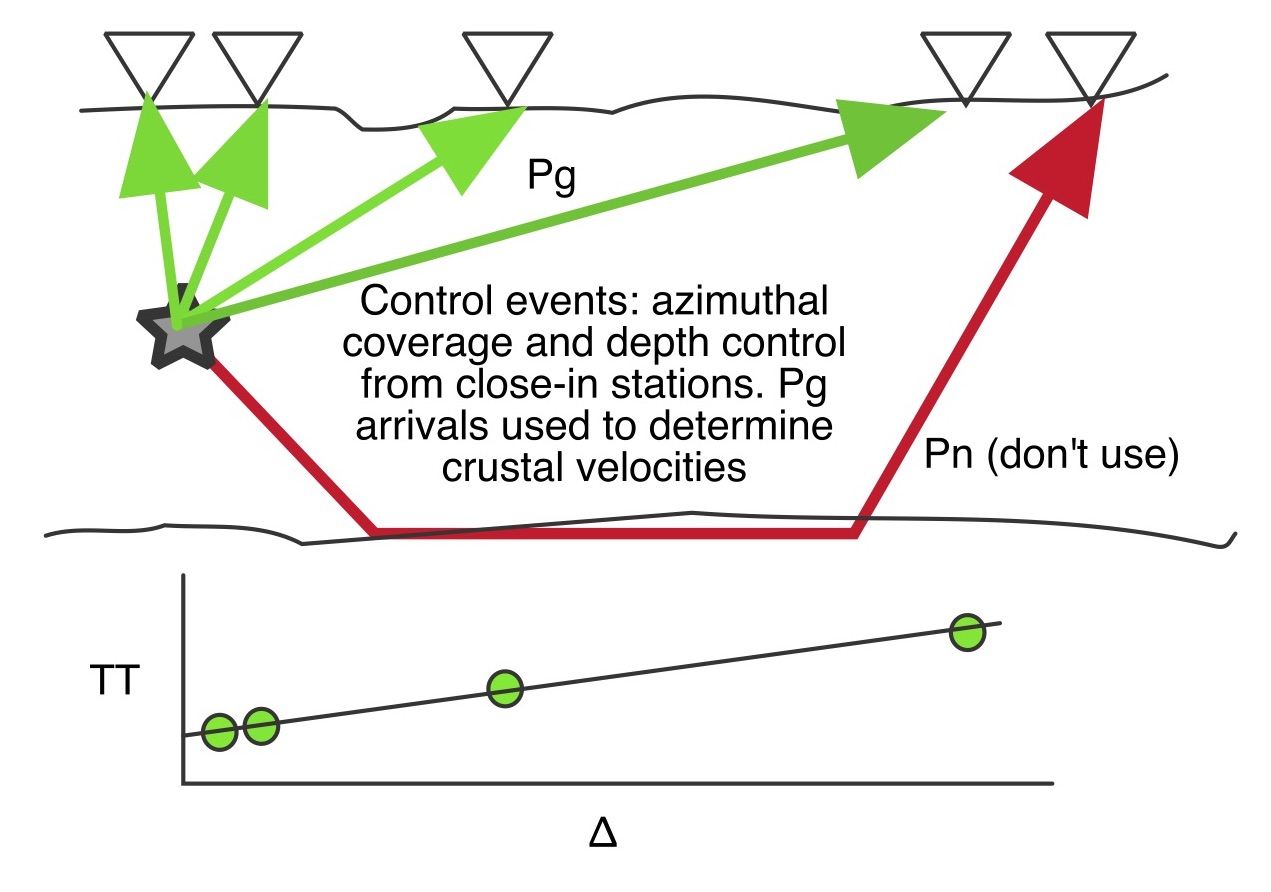
The “don’t use” label for the Pn arrival in this cartoon refers to depth control and determination of the hypocentroid. It is fine to use all phases to constrain the cluster vectors. “Refining the crustal velocity model” is not as tricky as it sounds. Very few clusters have ever required more than two layers in the crustal model and a single layer crustal model works quite well for many. It requires much denser data sets than we usually have for mloc to resolve more detail in the crustal model and then it still makes very little difference in the final locations.
Next, considering the Pn arrivals for the control events, the thickness of the crust (Moho depth) and upper mantle velocity can be constrained. In continental regions it usually needs to be a bit thicker than the 35-km thick crust used in ak135.
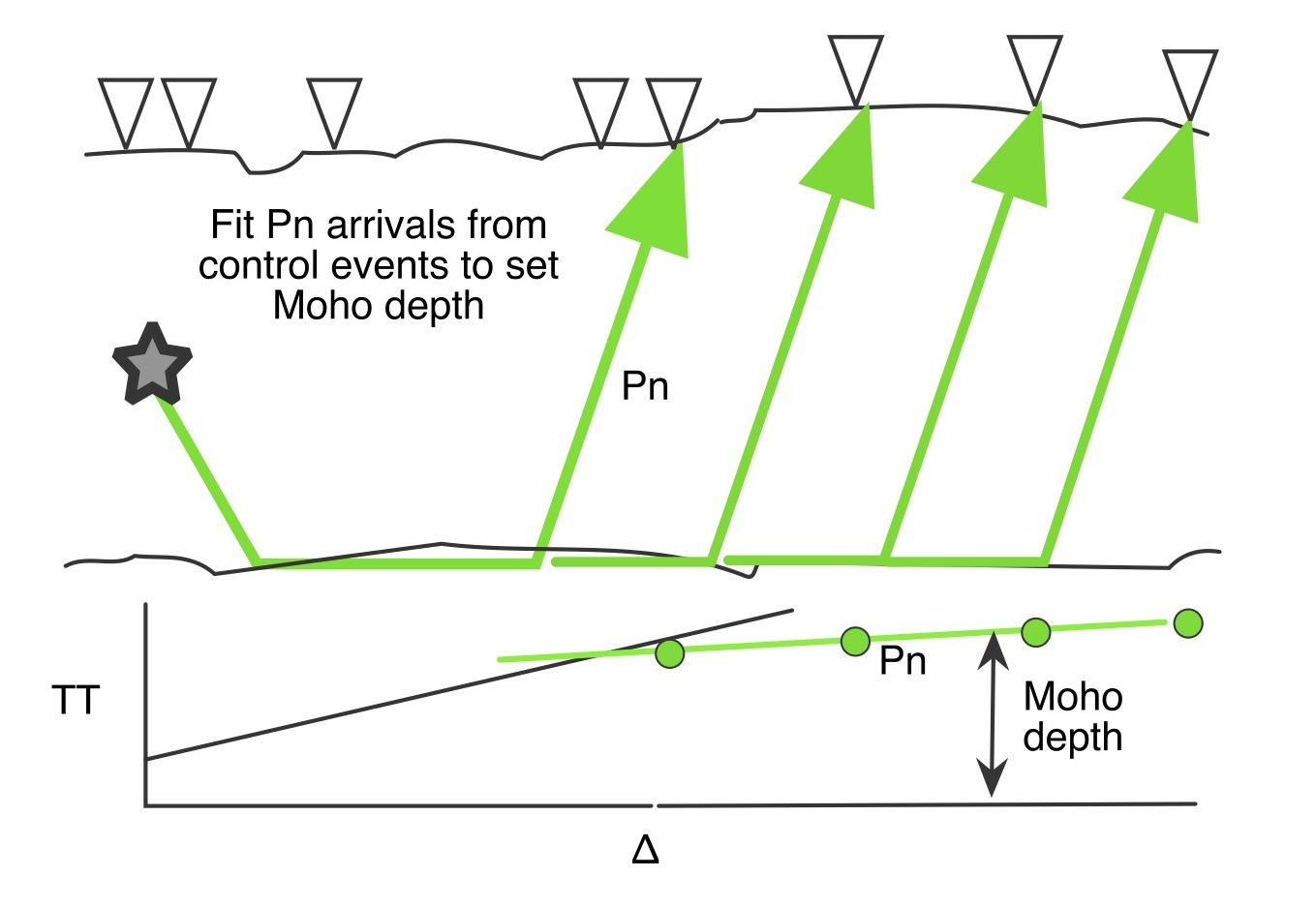
Our non-control event may have only a few direct crustal arrivals, and those at distances beyond what is normally needed for depth constraint (so ∂t/∂h is near zero). If such an event is added to the subcluster of control events, its origin time will be driven by the fit of its Pn readings (steep take-off angles) to those of the control events, for the assumed focal depth.
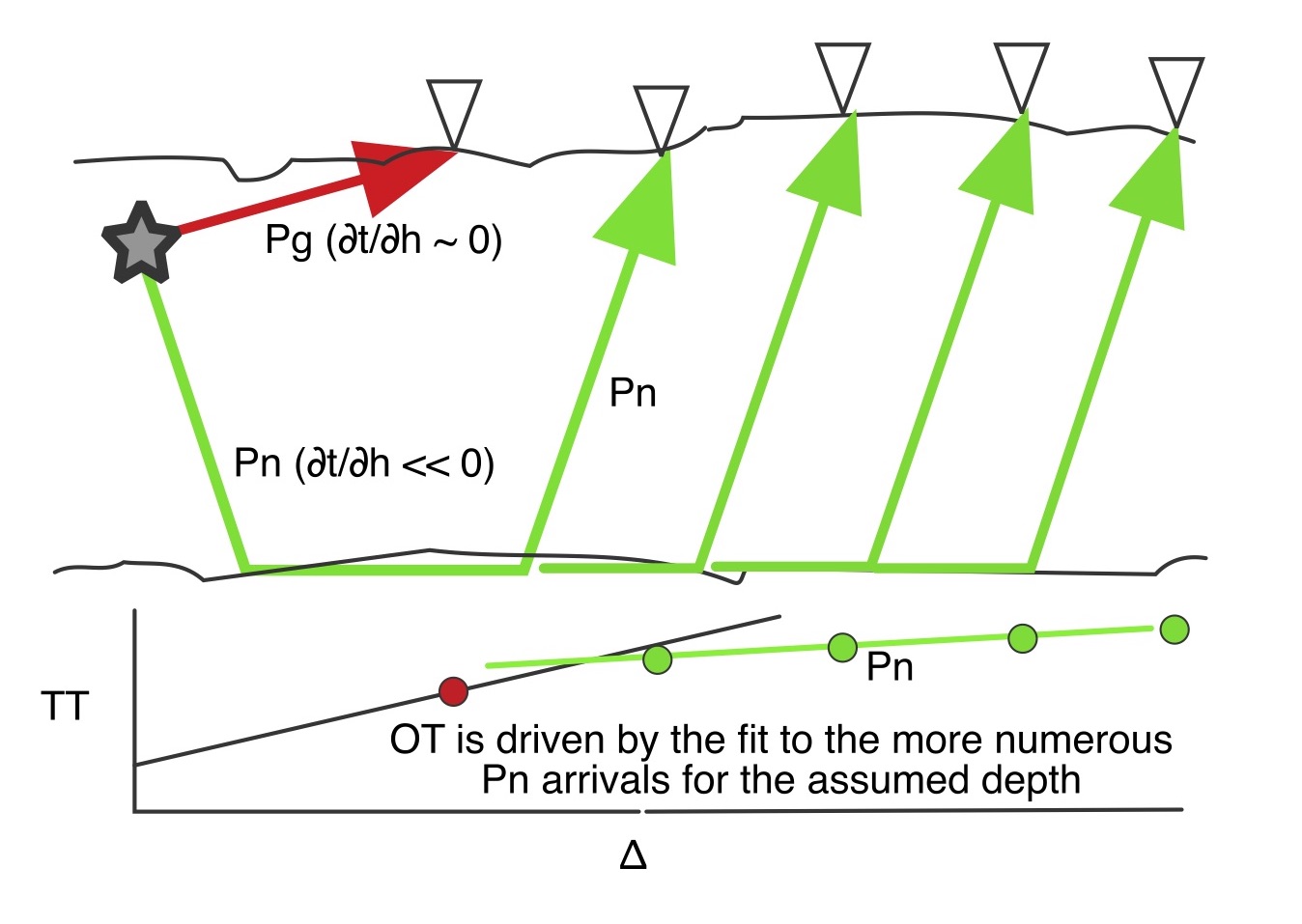
What happens with different assumed depths for our non-control event? If the assumed depth is too great, the origin time must be later to still fit the Pn arrivals with shorter raypaths. The Pg arrival time has almost no dependence on depth (raypath length stays the same) but its residual is affected by changes in origin time. A later origin time makes the theoretical arrival time later, causing a negative residual for the observed arrival, the same sense as if the event were too far from the station. If this were a station on top of the event, we would say the focus should be shallower (closer to the station). The opposite occurs for shallower assumed depths, yielding a positive residual for the observed arrival. Focal depth of our non-control event is adjusted so that the direct arrivals are consistent with the travel-time model for crustal arrivals based on the control events.
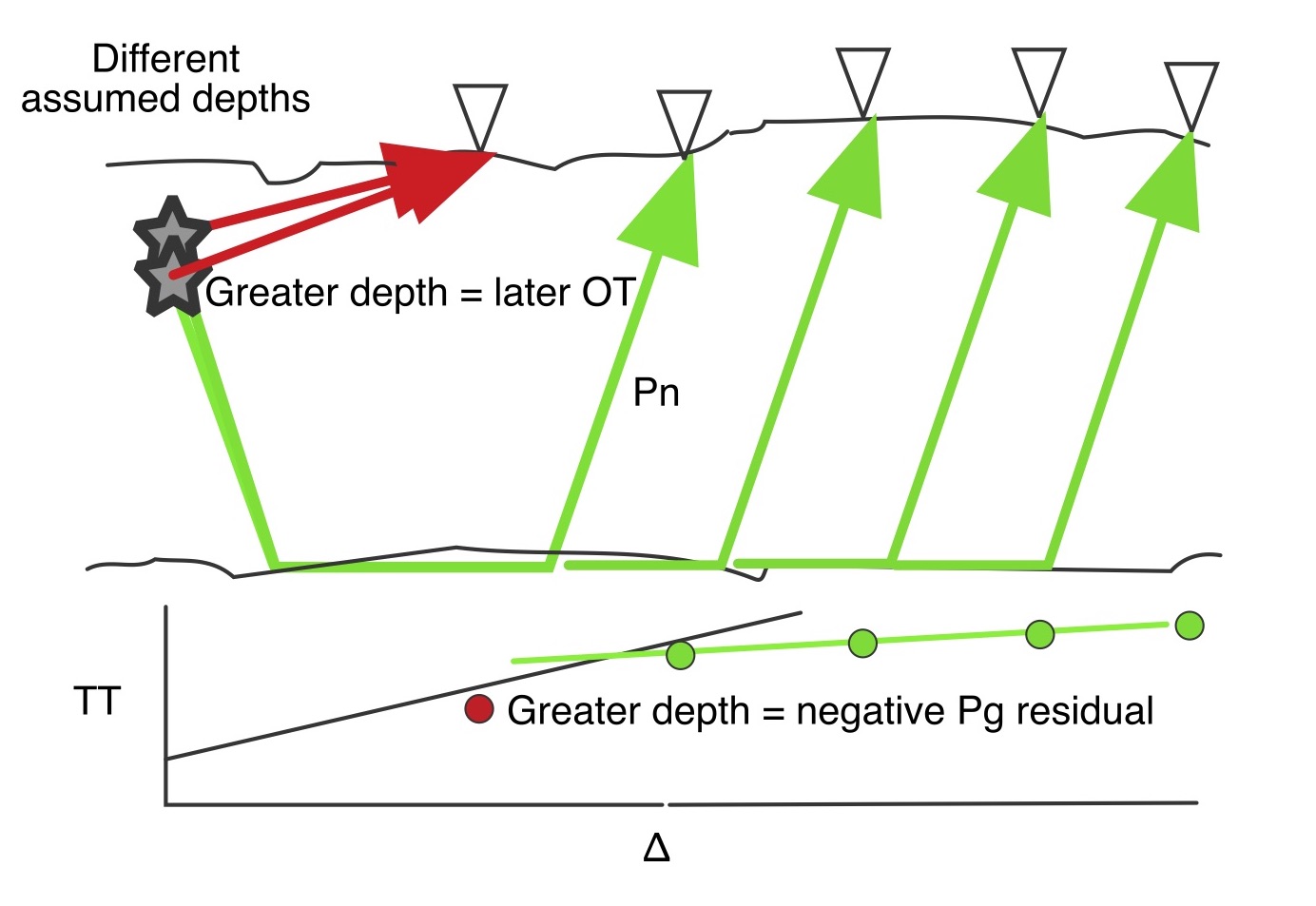
The sensitivity of this method of constraining focal depth is not as high as the use of near-source arrivals, but it is still quite useful because it is so widely applicable. As a rule of thumb, when the depth is constrained with the local-distance method (command depl) I usually give it an uncertainty of 4 km, as compared to 3 km for depths constrained by near-source readings. Obviously, confidence will be higher when there are more data points. There are many cases in which events have readings over the entire distance range where direct crustal arrivals are the first-arriving phases, so it does not take long to develop a feel for the sensitivity of the two types of data to focal depth.
It is not just the Pn data that drive the change in origin time when focal depth is changed; all arrivals have some effect on this. For most events, however, the Pn data are the dominant influence. Except for the very largest events they are usually the most numerous and they normally have small empirical reading errors, leading to large importance in the inversion.
It is very important to remember the sequence that must be followed for this method to work:
- Identify control events, usually after an initial run of mloc.
- Working only with control events, do additional runs in direct calibration mode (preferably free depth inversions but fixed depth works too), using only direct-arriving crustal phases for the hypocentroid (command hlim), adjusting the crustal velocity model and focal depths. Cleaning of outliers of the direct-arriving crustal phases is done now also.
- When the crustal model and focal depths of the control events are stable, consider the Pn data and adjust the crustal thickness to match the data. The baseline offset of Pn phase in the .ttsprd file can be helpful.
- Now non-control events that have at least one direct crustal arrival can be added (a few at a time is best) to the cluster, adjusting focal depth to obtain ~zero mean for the residuals of whatever direct-arriving crustal phases are available. Initial cleaning of outliers in the direct-arriving crustal phase dataset is done now.
- Try to avoid changing the crustal model after this point. If you do, you may need to go through these steps again.
Uncertainty of Focal Depth
Among the methods of constraining focal depth discussed here, reasonably objective measures of uncertainty are obtained from free-depth relocations and from the analysis of teleseismic depth phases, with the caveat that these estimates are influenced by the degree to which outlier readings have been handled correctly. For depths set according to the fit to near-source readings or local-distance readings, the uncertainty will be a subjective matter. There is no uncertainty associated with depths set according to a cluster default depth (command depc).
Free-Depth
The calculated uncertainty in focal depth of a free-depth relocation can be found in the ~.summary file and the ~.hdf file. Typical values are 0.5 to 3.0 km.
Teleseismic Depth Phases
For estimates of focal depth based on teleseismic depth phases, which are analyzed as relative depth phases in mloc, the uncertainties can vary greatly; in general uncertainty scales with depth because of the near total lack of confidence in reported phase identifications and the increasing separation of pP and sP arrival times with depth. For shallower events it matters less whether an arrival is actually a pP or sP phase. As always, having more samples helps. In practice, the depths determined with 3 or more consistent depth phases from different stations generally agree well with estimates of focal depth from other sources and with common sense.
The uncertainties in focal depths estimated from relative depth phases are usually asymmetric because there are usually two minima in the misfit function that are close to each other. The algorithm tests for the global minimum at 1-km depth increments so in the case of a single depth phase that could be either pP or sP, the choice of one over the other as the “best” is random. In setting a depth constraint with a depd command the user can decide that the other minimum is more likely, given what else is known about the depth range of the cluster’s events, and restate the uncertainty accordingly. This is most easily done from the relative depth phase plot (rdpp command).
For larger events with many reported depth phases, the ambiguity of phase ID often collapses into a single well-defined minimum with an uncertainty of ±3-4 km.
Near-Source Readings
When judging the uncertainty of a focal depth determined by the fit to arrivals from near-source stations there are several matters to consider:
- For shallow events the raypath will be exclusively in the uppermost part of the crust, whose velocity structure is effectively impossible to constrain with the kind of data used in mloc. The velocity in the assumed crustal model may be quite wrong (usually too fast, so the focus will be forced deeper). On the other hand the raypath is very short, so maybe the amount of bias is small.
- Picking the arrival of a larger event at very short distance may be easy for the analyst but it may not be the signal that is observed and picked at stations further away. This tends to lead to negative residuals for the very closest stations, thus estimates of depth that are too shallow.
I usually assign an uncertainty of ±3 km to these estimates of focal depth. When both Pg and Sg readings are present and consistent, or if there are several stations within range, a smaller uncertainty can be contemplated but I think ±2 km is about the limit.
Local Distance Readings
The local distance method of constraining depth is subject to greater uncertainty than the near-source method, especially when the only available readings are at larger distances, say 70-100 km. I routinely assign local distance estimates an uncertainty of ±4 km, but there are certainly cases where a larger value could be justified.
