Calibration
In the context of earthquake location, we use the term calibration to refer to an analysis that includes procedures to minimize the biasing effect of unknown Earth structure (i.e., velocity variations) on hypocentral parameters and also incorporates procedures to obtain realistic measures of uncertainty of those parameters. Two major challenges in this regard are 1) to reduce the biasing effect of outlier readings in a least-squares estimation procedure, and 2) to minimize the biasing effects of unknown data variances on estimates of the uncertainty of the hypocentral parameters.
Two methods for determining calibrated locations for clusters of earthquakes are implemented in mloc. The key to calibrated locations is the use of near-source data to establish the location of the cluster in absolute spatial and temporal coordinates. One method of calibration (indirect calibration) is based on external (a priori) information on the location of one or more cluster events. Such information can be derived from seismological, geological, or remote sensing data. The second method of calibration (direct calibration) is based on analysis of a subset of the arrival time information in the cluster at short epicentral distances.
The second aspect of calibration, realistic uncertainties, is achieved in both direct and indirect methods of calibration by a careful analysis of empirical readings errors (derived from the actual arrival time data) which are used both for weighting in the inversion for location and also for identifying outlier readings, often referred to as “cleaning”. These subjects are discussed in other sections of the website. In the rest of this section we describe the direct and indirect methods of calibration and the feature of the hypocentroidal decomposition method of multiple event relocation which makes it especially well-suited to this kind of analysis.
Applicability
The methods of location calibration described here can be used at a range of scales, from a handful of small events recorded locally to several hundred large events recorded globally. The algorithm is best-suited for data sets of about 200 events or less, and it is desirable to restrict the geographic extent of a cluster to approximately 100 km or less. There must be a minimal level of “connectivity” between events in a cluster, meaning repeated observations by the same seismic station. Since calibration depends on data at short range from the source, it is not possible to calibrate the locations of deep earthquakes, although the relative locations can be improved.
Calibrated locations with uncertainties of 2-3 km in epicenter are achievable with either method, as can be seen by reviewing the results posted at the GCCEL website.
Hypocentroidal Decomposition
The location calibration analysis is based on the Hypocentroidal Decomposition (HD) method for multiple event relocation introduced and by Jordan and Sverdrup (1981). The basic algorithm is completely described in that reference. The essence of the HD algorithm is the use of orthogonal projection operators to separate the relocation problem into two parts:
- The cluster vectors, which describe the relative locations in space and time of each event in the cluster. They are defined in kilometers and seconds, relative to the current position of the hypocentroid.
- The hypocentroid, which is defined as the centroid of the current locations of the cluster events. It is defined in geographic coordinates and Coordinated Universal Time (UTC).
Both methods of calibration described here depend fundamentally on this decomposition of the relocation problem. Similar approaches could conceivably be implemented in other multiple event relocation algorithms but it seems likely to be considerably more difficult than it is with hypocentroidal decomposition.
The cluster vectors are defined only in relation to the hypocentroid. The hypocentroid can be thought of as a virtual event with geographic coordinates and origin time in UTC. The orthogonal projection operators act on the data set of arrival times to produce a data set that includes only data that actually bears on the relative location of cluster events, i.e., multiple reports of a given seismic phase at the same station for two or more events in the cluster.
The hypocentroid is located very much as an earthquake would be, except that the data are drawn from all the cluster events. Thus it is typical for the hypocentroid to be determined by many thousands of readings. Nevertheless, the hypocentroid is subject to unknown bias because the theoretical travel times (typically ak135) do not fully account for the three-dimensional velocity structure of the Earth. Geographic locations for the cluster events are found by adding the cluster vectors to the hypocentroid.
The HD method works iteratively. At each iteration, two inversions are performed, first for the cluster vectors relative to the current hypocentroid, then for an improved hypocentroid. The cluster vectors are added to the new hypocentroid to obtain updated absolute coordinates for each event. The convergence criteria are based on the change in relative location of each event (0.5 km) and the change in the hypocentroid (0.005°). The convergence limits for origin time and depth, for cluster vectors and hypocentroid, are 0.1 s and 0.5 km, respectively. Convergence is normally reached in 2 or 3 iterations.
The data sets used for the two problems need not be (and usually are not) the same. Because the inverse problem for changes in cluster vectors is based solely on arrival time differences, baseline errors in the theoretical travel times drop out and it is desirable to use all available phases at all distances outside the immediate source region. For the hypocentroid, baseline errors in theoretical travel times are more important and one may wish to limit the data set to a phase set, e.g., teleseismic P arrivals in the range 30-90°, to achieve a more stable (but uncalibrated) result. The choice of data set for determining the hypocentroid has great importance in the “direct” calibration method described below.
Similarly, weighting schemes are different for the two inversions, reflecting the different natures of the two problems. Empirical reading errors for each station-phase pair are used in weighting data for estimating both the hypocentroid and cluster vectors, but the uncertainty of the theoretical travel times, which are estimated empirically for each phase from the residuals of previous runs, is relevant only to the hypocentroid.
Until this point the HD algorithm is used only to obtain improved relative locations for the cluster events, with a geographic location for the cluster as a whole (the hypocentroid) that is biased to an unknown degree by unmodeled Earth structure that has been convolved with the (typically) unbalanced geographic distribution of reporting seismic stations. The calibration process attempts to minimize this bias.
Calibration of a cluster is done in two ways, which we refer to as “indirect” and “direct” calibration.
Indirect Calibration
If the location and origin time of one or more of the cluster events can be specified with high accuracy from independent information, we can calibrate the entire cluster by shifting it in space and time to optimally match the known location of the calibration event(s). The approach is illustrated in this cartoon.
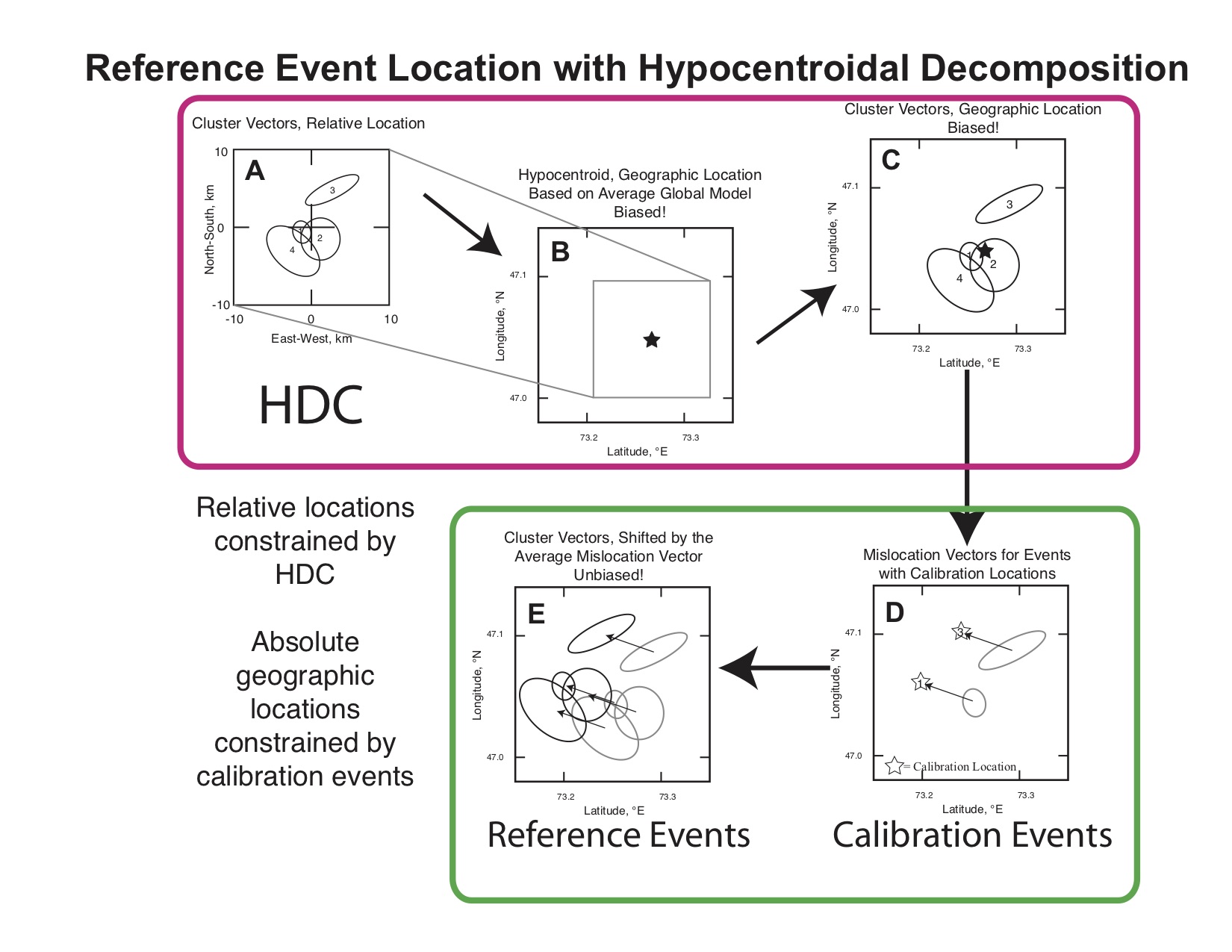
The steps inside the red box represent standard, uncalibrated relocation with mloc. The steps inside the green box represent the calibration analysis.
- A: Cluster vectors (relative locations) estimated.
- B: Hypocentroid estimated but known to be biased by unknown Earth structure.
- C: Add cluster vectors to hypocentroid, yielding uncalibrated estimates of hypocenters of individual events.
- D: An average “calibration shift” is calculated from comparison with a subset of “known” locations.
- E: All events shifted to obtain calibrated hypocenters.
A common source of such independent information is a temporary seismic network deployment that captures an event with a large number of stations at very short epicentral distances, and which is also large enough to be well recorded at the distances at which other events in the cluster were observed (usually, regional and teleseismic distances). Aftershock studies are a frequent source of such data. If it is possible to obtain the temporary network arrival time data a direct calibration analysis would be preferred, but sometimes only the hypocenters are available. InSAR data is also used for this purpose, but this requires the use of at least some seismic data at short distance to calibrate origin time. The other problem with InSAR analysis is that it is difficult to specify where along an extended source the epicenter should be placed. In some cases mapped faulting from large events can be used to help constrain the location of calibration events, but this also suffers from the uncertainty about where along an extended source to place the epicenter.
When we use the indirect calibration approach we must take into account the uncertainty of the calibration locations, and when there is more than one calibration event we also include a contribution to uncertainty to reflect any discrepancy between the relative locations of the calibration events and the cluster vectors of the corresponding events.
Direct Calibration
It is often the case that there are a few permanent seismic stations close to a cluster of earthquakes, but that no single event is well-enough recorded to reach the level of accuracy necessary to serve as a calibration event. On the other hand, the handful of local seismic stations may have recorded many events in the cluster, so that the number of “short distance” readings is rather large, and well-enough distributed to allow the hypocentroid to be located using only these data. The direct calibration method is based on the use of arrival time data from nearby stations to locate the hypocentroid. By keeping raypaths short, accumulated error in the theoretical travel times (and thus, location bias) is minimized.
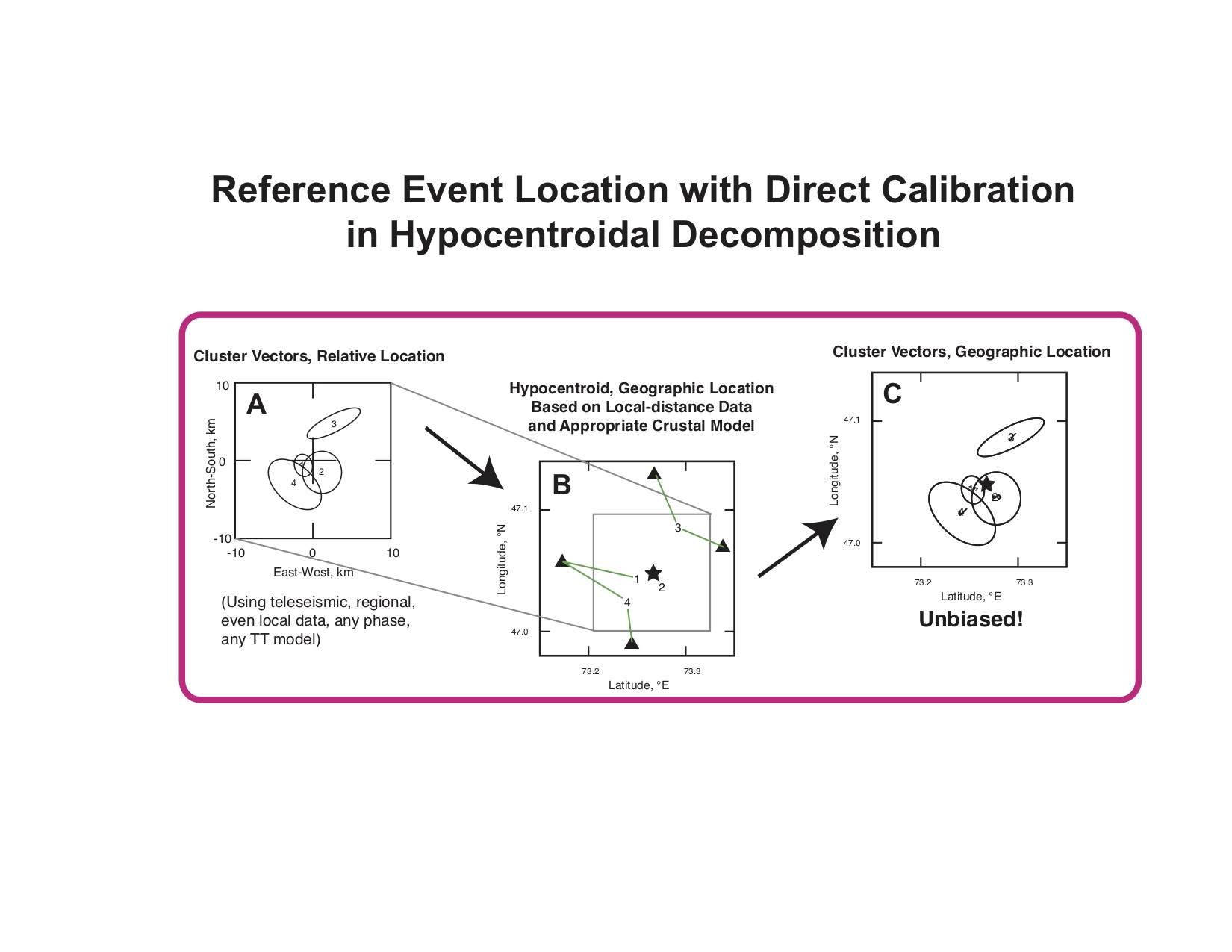
- A: Cluster vectors (relative locations) estimated.
- B: Hypocentroid estimated from close-in stations, thus minimizing location bias.
- C: Add cluster vectors to hypocentroid, yielding calibrated estimates of hypocenters of individual events.
In any case where we have the data to locate one or more calibration events for the indirect method, we also have the option to use those same data in the direct calibration method. The decision on which to use is made on a case-by-case basis, because characteristics of the data sets may lead to a better result with one method than the other. Of course, if we are using InSAR data or other remote sensing or geological information to constrain the calibration, we must use the indirect method.
In mloc it is possible to set up a relocation which uses both methods. Direct calibration will be done as part of the normal relocation process and then the adjustment for indirect calibration will be made, relative to whatever calibration locations have been declared. Some output files will be written for each method, but the .summary file will take the indirect calibration as preferred, as will the summary plots. It is quite useful to have both estimates of calibration as a measure of quality control.
